Topological Sort. Algorithms Series

Topological sort can be applied in scheduling problems.

Those types of problems can be solved when:

tasks and precedence constraints are defined;
cycles are detected and removed.

Implementation of cycle detection can be found here.

Test should check that reverse post order is correct.

    @Test
    void shouldReturnPostOrder() {
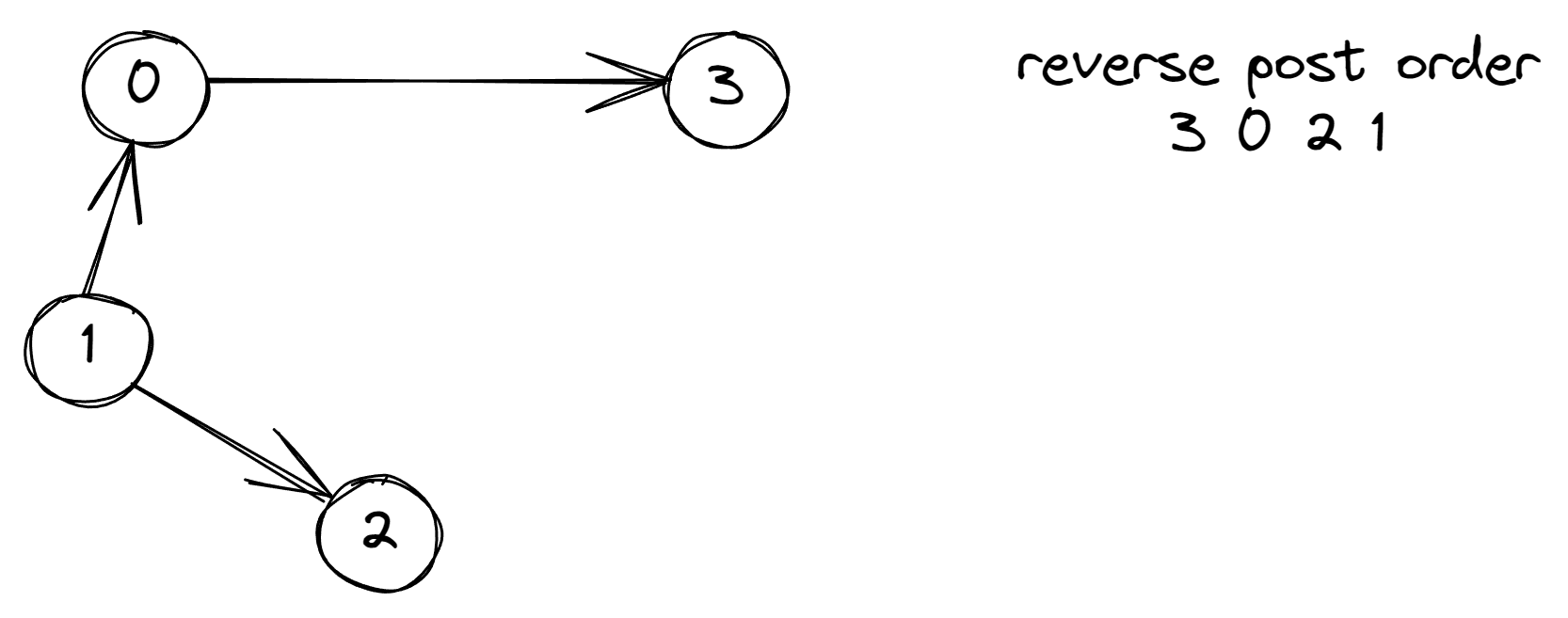
        DirectedGraph directedGraph = new DirectedGraph(4);
        directedGraph.addEdge(1, 0);
        directedGraph.addEdge(0, 3);
        directedGraph.addEdge(1, 2);

        TopologicalSort topologicalSort = new TopologicalSort(directedGraph);
        LinkedList<Integer> expected = new LinkedList<>(Arrays.asList(3, 0, 2, 1));

        assertEquals(expected, topologicalSort.getReversePostOrder());
    }

This problem can be solved quite elegantly with the use of DFS (Depth First Search). To get the reverse post order we need to put the vertex on stack (linked list) after the recursive call.

public class TopologicalSort {
    private final boolean[] visited;

    List<Integer> postOrder;

    public TopologicalSort(DirectedGraph graph) {
        visited = new boolean[graph.getNumberOfVertices()];
        postOrder = new LinkedList<>();
        for (int ver = 0; ver < graph.getNumberOfVertices(); ver++) {
            if (!visited[ver]) {
                dfs(graph, ver);

            }

        }
    }

    private void dfs(DirectedGraph graph, int vertex) {
        visited[vertex] = true;
        for (int conVer : graph.getConnectionsFor(vertex)) {
            if (!visited[conVer]) {
                dfs(graph, conVer);
            }
        }
        postOrder.add(vertex);
    }

    public List<Integer> getReversePostOrder() {
        return postOrder;
    }

Complete implementation with test cases can be found on GitHub.

Sources: