Red Black Binary Search Tree: Part 2 delete. Algorithms Series

To implement delete() method we need to take care about helper methods first. First we will take a look at deleteMin().

DELETE MIN

Test cases for deleteMin() should check that:

minimal element is not present
tree is balanced, which means:
- there is no more than 1 left RED links in the row
- there is no right RED link
- root should be always BLACK

    @Test
    void shouldDeleteMinElement() {
        RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        brBinarySearchTree.deleteMin();

        assertNull(brBinarySearchTree.get(8));
    }

    @Test
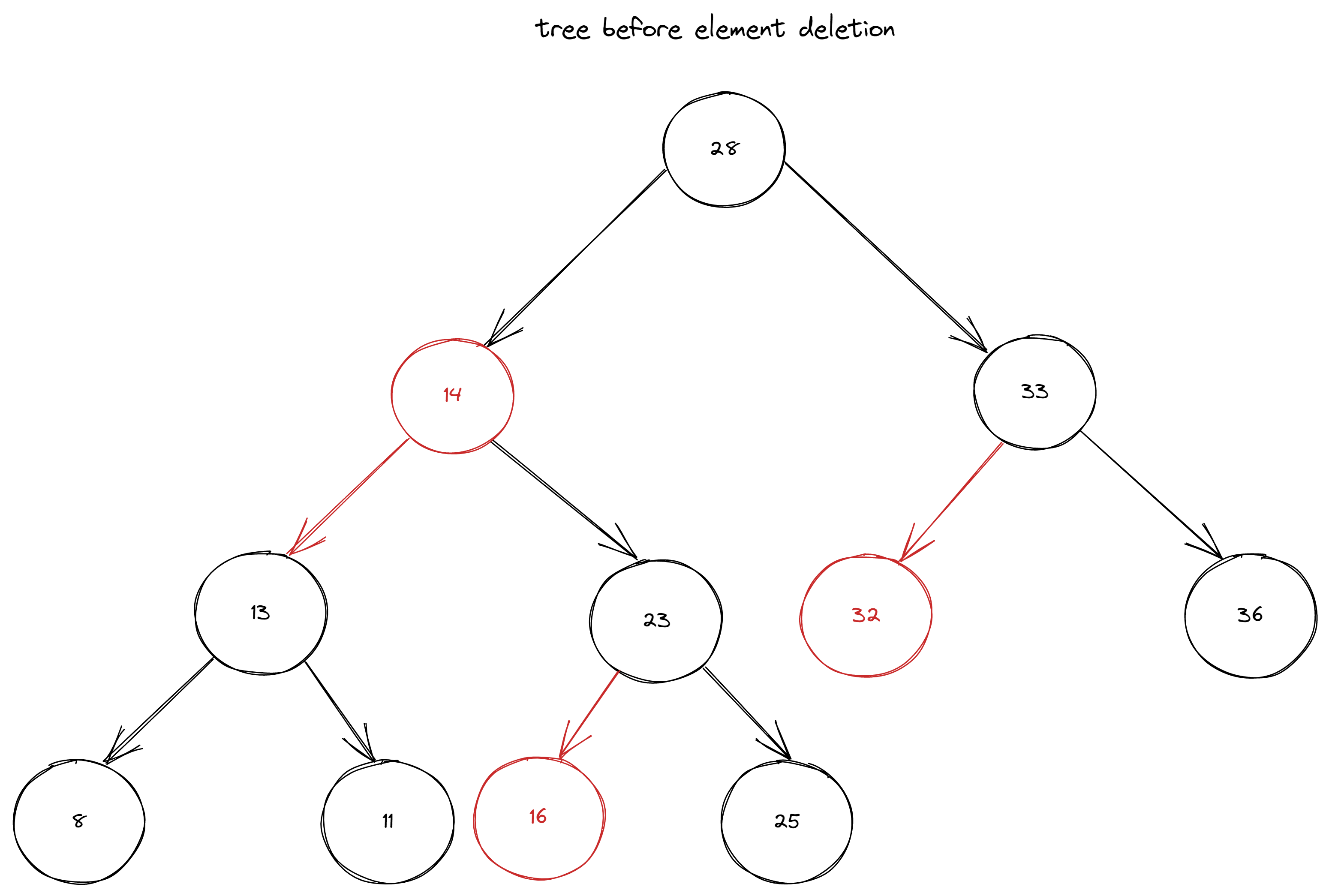
    void treeShouldBeRebalancedAfterDeleteMin() {
        RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        brBinarySearchTree.deleteMin();

        assertEquals("23", brBinarySearchTree.root.left.value);
        assertFalse(brBinarySearchTree.root.left.color, "Should be black");

        assertEquals("14", brBinarySearchTree.root.left.left.value);
        assertTrue(brBinarySearchTree.root.left.left.color, "Should be red");

        assertEquals("13", brBinarySearchTree.root.left.left.left.value);
        assertFalse(brBinarySearchTree.root.left.left.left.color, "Should be black ");

        assertEquals("25", brBinarySearchTree.root.left.right.value);
        assertFalse(brBinarySearchTree.root.left.right.color, "Should be black");
    }

2 more helper methods for achieving balance will be moveRedLeft() and moveRedRight().

private Node moveRedLeft(Node node) {
        flipColors(node);
        if (isRed(node.right.left)) {
            node.right = rotateRight(node.right);
            node = rotateLeft(node);
            flipColors(node);
        }
        return node;
    }

    private Node moveRedRight(Node node) {
        flipColors(node);
        if (isRed(node.left.left)) {
            node = rotateRight(node);
            flipColors(node);
        }
        return node;
    }

With helper methods in place we can move on with implementation.

    public void deleteMin() {
        if (!isRed(root.left) && !isRed(root.right))
        root.color = RED;

        root = deleteMin(root);
        if (root != null) root.color = BLACK;
        }

    private Node deleteMin(Node node) {
        if (node.left == null)
            return null;

        if (!isRed(node.left) && !isRed(node.left.left))
            node = moveRedLeft(node);

        node.left = deleteMin(node.left);
        return balanceBST(node);
    }

DELETE

Test cases for delete() will be similar to deleteMin(). They should check:

given key is not present
tree is rebalanced

    @Test
    void shouldDeleteElementByKey() {
        RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        brBinarySearchTree.delete(32);

        assertNull(brBinarySearchTree.get(32));
    }

    @Test
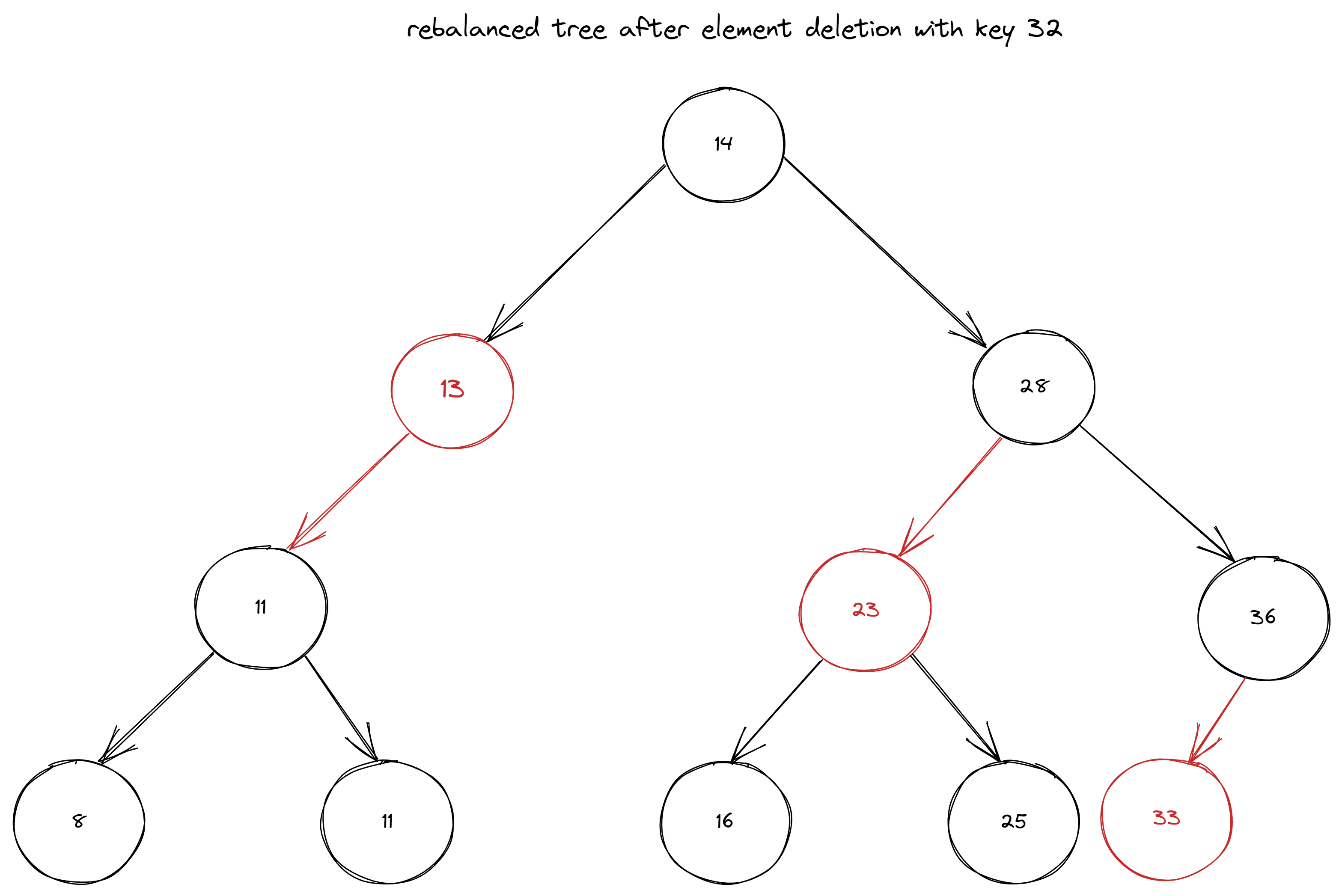
    void treeShouldBeRebalancedAfterDelete() {
        RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        brBinarySearchTree.delete(32);
        assertEquals("14", brBinarySearchTree.root.value);

        assertEquals("28", brBinarySearchTree.root.right.value);
        assertFalse(brBinarySearchTree.root.right.color, "Should be black");

        assertEquals("23", brBinarySearchTree.root.right.left.value);
        assertTrue(brBinarySearchTree.root.right.left.color, "Should be red");

        assertEquals("33", brBinarySearchTree.root.right.right.left.value);
        assertTrue(brBinarySearchTree.root.right.right.left.color, "Should be red");
    }

Deletion implementation is based on deletion of simple BST. It gets a bit more complicated because we need to keep the balance.

    public void delete(Key key) {
        if (!isRed(root.left) && !isRed(root.right))
            root.color = RED;

        root = delete(root, key);
        if (root != null) root.color = BLACK;
    }

    private Node delete(Node node, Key key) {
        if (key.compareTo(node.key) < 0) {
            if (!isRed(node.left) && !isRed(node.left.left))
                node = moveRedLeft(node);
            node.left = delete(node.left, key);
        } else {
            if (isRed(node.left))
                node = rotateRight(node);
            if (key.compareTo(node.key) == 0 && (node.right == null))
                return null;
            if (!isRed(node.right) && !isRed(node.right.left))
                node = moveRedRight(node);
            if (key.compareTo(node.key) == 0) {
                Node x = min(node.right);
                node.key = x.key;
                node.value = x.value;
                node.right = deleteMin(node.right);
            } else node.right = delete(node.right, key);
        }
        return balanceBST(node);
    }

Complete implementation with test cases can be found on GitHub.

Sources: