Red Black Binary Search Tree: Part 1 put. Algorithms Series

Red-Black Tree is a Binary Search Tree with one extra bit of storage per node - color, which can be either RED or BLACK. We need it to keep BST “balanced”, that means basic dynamic set operations will be fast (guaranteed time O(lg n) ).

Red-black tree has next properties:

Every node is RED or BLACK
The root id always BlACK
Every null leaf is black
If a node is RED, then both children are BLACK
For each node, all simple paths from the node to descendant leaves contain the same number of BLACK nodes.

To get started with test cases we need a skeleton first.

public class RedBlackBinarySearchTree<Key extends Comparable<Key>, Value> {
    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private Node root;

    protected class Node {
        protected Key key;
        protected Value value;
        protected Node right;
        protected Node left;
        protected int nodeNumber;
        protected boolean color;

        protected Node(Key key, Value value, int nodeNumber, boolean color) {
            this.key = key;
            this.value = value;
            this.nodeNumber = nodeNumber;
            this.color = color;
        }

    }

    protected boolean isRed(Node node) {
        if (node == null) {
            return false;
        }
        return node.color == RED;
    }

}

Methods get() and size() are the same as in Binary search tree.

PUT

Test cases for put should check that:

value is present
there is no more than 1 left RED links in the row
there is no right RED link
root should be always BLACK

   @Test
    void valueShouldBePresentWhenPut() {
            RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = new RedBlackBinarySearchTree<>();
        brBinarySearchTree.put(15, "AnyValue");

        assertEquals("AnyValue", brBinarySearchTree.get(15));
        }

    @Test
    void rootShouldBeBlack() {
            RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        assertEquals("28", brBinarySearchTree.root.value);
        assertFalse(brBinarySearchTree.root.color, "Root should be black");
        }

    @Test
    void leftLinkShouldBeRed() {
            RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        assertEquals("14", brBinarySearchTree.root.left.value);
        assertTrue(brBinarySearchTree.root.left.color, "Should be red");
        }

    @Test
    void shouldBeNoMoreThanOneLeftRedLinkInARow() {
            RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = createRedBlackBST();

        assertEquals("11", brBinarySearchTree.root.left.left.value);
        assertFalse(brBinarySearchTree.root.left.left.color, "Should not be 2 red left in a row");
        }

    private RedBlackBinarySearchTree<Integer, String> createRedBlackBST() {
        RedBlackBinarySearchTree<Integer, String> brBinarySearchTree = new RedBlackBinarySearchTree<>();
        brBinarySearchTree.put(8, "8");
        brBinarySearchTree.put(11, "11");
        brBinarySearchTree.put(14, "14");
        brBinarySearchTree.put(13, "13");
        brBinarySearchTree.put(16, "16");
        brBinarySearchTree.put(23, "23");
        brBinarySearchTree.put(25, "25");
        brBinarySearchTree.put(28, "28");
        brBinarySearchTree.put(32, "32");
        brBinarySearchTree.put(33, "33");
        brBinarySearchTree.put(36, "36");
        return brBinarySearchTree;
        }

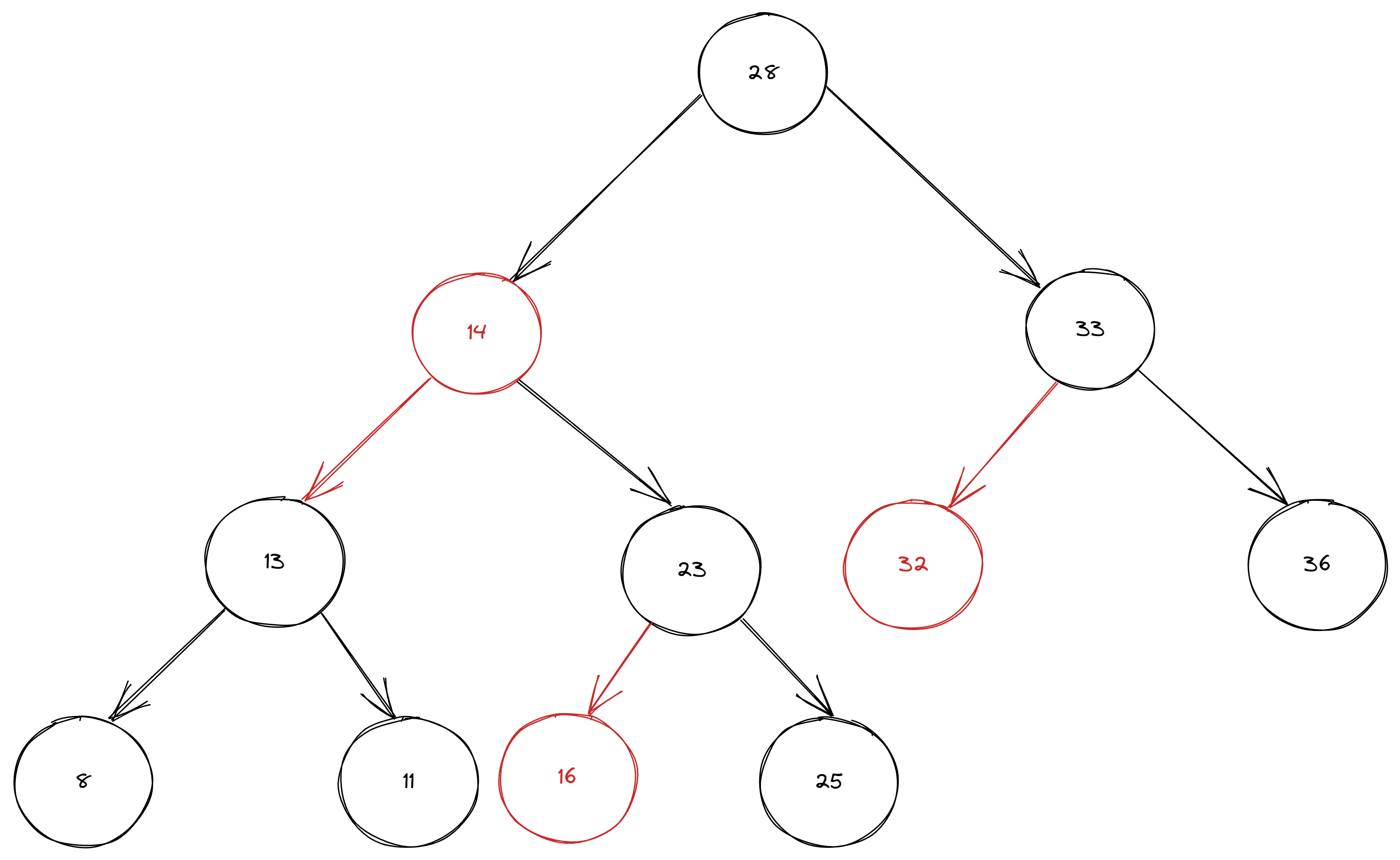
Code for the implementation of put() method is very similar to BST implementation except conditions that balance tree. To achieve balance we need to implement rotateLeft(), rotateRight() and flipColors() methods first.

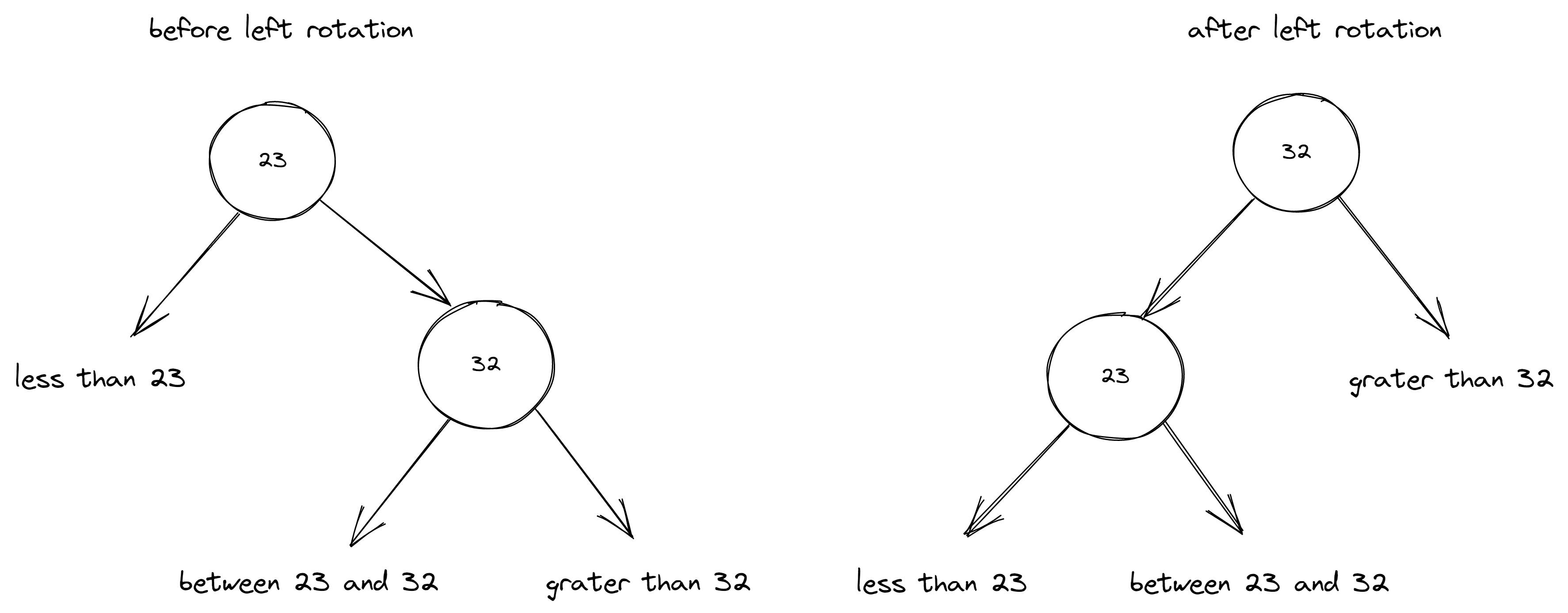
    private Node rotateLeft(Node node) {
        Node nodeToRotate = node.right;
        node.right = nodeToRotate.left;
        nodeToRotate.left = node;
        nodeToRotate.color = node.color;
        node.color = RED;
        nodeToRotate.nodeNumber = node.nodeNumber;
        node.nodeNumber = 1 + size(node.left) + size(node.right);
        return nodeToRotate;
        }

 private Node rotateRight(Node node) {
        Node nodeToRotate = node.left;
        node.left = nodeToRotate.right;
        nodeToRotate.right = node;
        nodeToRotate.color = node.color;
        node.color = RED;
        nodeToRotate.nodeNumber = node.nodeNumber;
        node.nodeNumber = 1 + size(node.left) + size(node.right);
        return nodeToRotate;
        }

private void flipColors(Node node) {
        node.color = RED;
        node.right.color = BLACK;
        node.left.color = BLACK;
        }

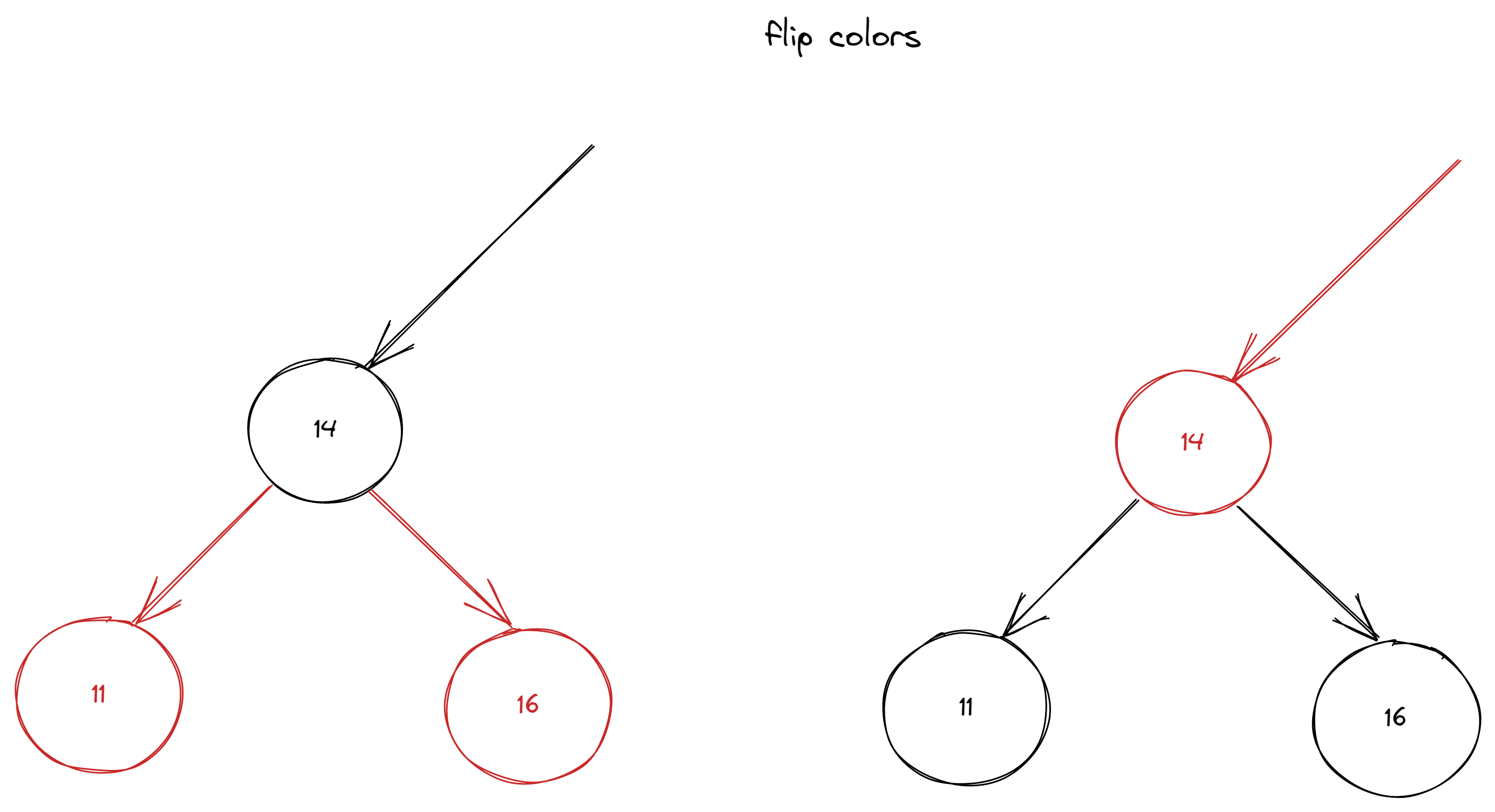
After those methods in place, we can complete the implementation.

    public void put(Key key, Value value) {
        root = put(root, key, value);
        root.color = BLACK;

    }

    private Node put(Node node, Key key, Value value) {
        if (node == null) {
            return new Node(key, value, 1, RED);
        }
        int compare = key.compareTo(node.key);
        if (compare < 0) {
            node.left = put(node.left, key, value);
        } else if (compare > 0) {
            node.right = put(node.right, key, value);
        } else {
            node.value = value;
        }
        if (isRed(node.right) && !isRed(node.left)) node = rotateLeft(node);
        if (isRed(node.left) && isRed(node.left.left)) node = rotateRight(node);
        if (isRed(node.left) && isRed(node.right)) flipColors(node);
        node.nodeNumber = size(node.left) + size(node.right) + 1;
        return node;
    }

Complete implementation with test cases can be found on GitHub.

Sources: