Binary Search Tree: Part 1 put, get, size. Algorithms Series

Development of computational infrastructure would not become available without effective searching algorithms. One type of such algorithms is symbol tables. Term symbol table is used to describe a mechanism where we can save information (value) and later retrieve it by specified key. Symbol tables sometimes also referred as dictionaries.

There are three main classic data structures that can support efficient symbol-table implementations: binary search trees, red -black trees and hash tables.

In this article we will dive into implementation of Binary Search Tree (BST).

To better understand implementation of BST, we will use TDD to test internal implementation. To get started with tests cases, we need a skeleton of BST. BST is a recursive data structure made up of nodes. Each node contains:

key
value
links to left and right nodes
number of nodes in subtree

Each node can have only one parent except root node, which has no parent.

public class BinarySearchTree<Key extends Comparable<Key>, Value> {

    protected Node root;

    protected class Node {
        protected Key key;
        protected Value value;
        protected Node left;
        protected Node right;
        protected int subtreeNodeNumber;

        public Node(Key key, Value value, int subtreeNodeNumber) {
            this.key = key;
            this.value = value;
            this.subtreeNodeNumber = subtreeNodeNumber;
        }
    }

    public int size() {
        return 0;
    }

    public Value get(Key key) {
        return null;
    }

    public void put(Key key, Value value) {
        return 0;
    }

}

This code will allow us to write tests that will fail first. Access modifiers “protected” is used for testing purposes only. In this part we will implement put, size and get functionality.

PUT

To check that put is working correctly we need next test cases:

left node should contain item with smaller key
right node should contain item with larger key
left node in the subtree should contain item with smaller key
size of BST is increased correctly

class BinarySearchTreeTest {

    public static final String LEFT_VALUE = "leftValue";
    public static final String ROOT_VALUE = "rootValue";
    public static final String RIGHT_VALUE = "rightValue";
    public static final int ROOT_KEY = 6;
    public static final int LEFT_KEY = 4;
    public static final int RIGHT_KEY = 8;
    public static final int SECOND_LEFT_KEY = 7;
    public static final String SECOND_LEFT_VALUE = "2LeftValue";

    @Test
    void leftLinkShouldPointToItemWithSmallerKey() {
        BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(LEFT_KEY, LEFT_VALUE);

        assertEquals(LEFT_KEY, bst.root.left.key);
        assertEquals(LEFT_VALUE, bst.root.left.value);
    }

    @Test
    void rightLinkShouldPointToItemWithLargerKey() {
        BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(RIGHT_KEY, RIGHT_VALUE);

        assertEquals(RIGHT_KEY, bst.root.right.key);
        assertEquals(RIGHT_VALUE, bst.root.right.value);
    }

    @Test
    void secondLeftLinkShouldPointToItemWithSmallerKey() {
        BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(RIGHT_KEY, RIGHT_VALUE);
        bst.put(SECOND_LEFT_KEY, SECOND_LEFT_VALUE);

        assertEquals(SECOND_LEFT_KEY, bst.root.right.left.key);
        assertEquals(SECOND_LEFT_VALUE, bst.root.right.left.value);
    }

    @Test
    void shouldReturnCorrectSizeOfBST() {
        BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(LEFT_KEY, LEFT_VALUE);
        bst.put(RIGHT_KEY, RIGHT_VALUE);

        assertEquals(3, bst.size());
    }
}

Representation of inserted in test values would look like this:

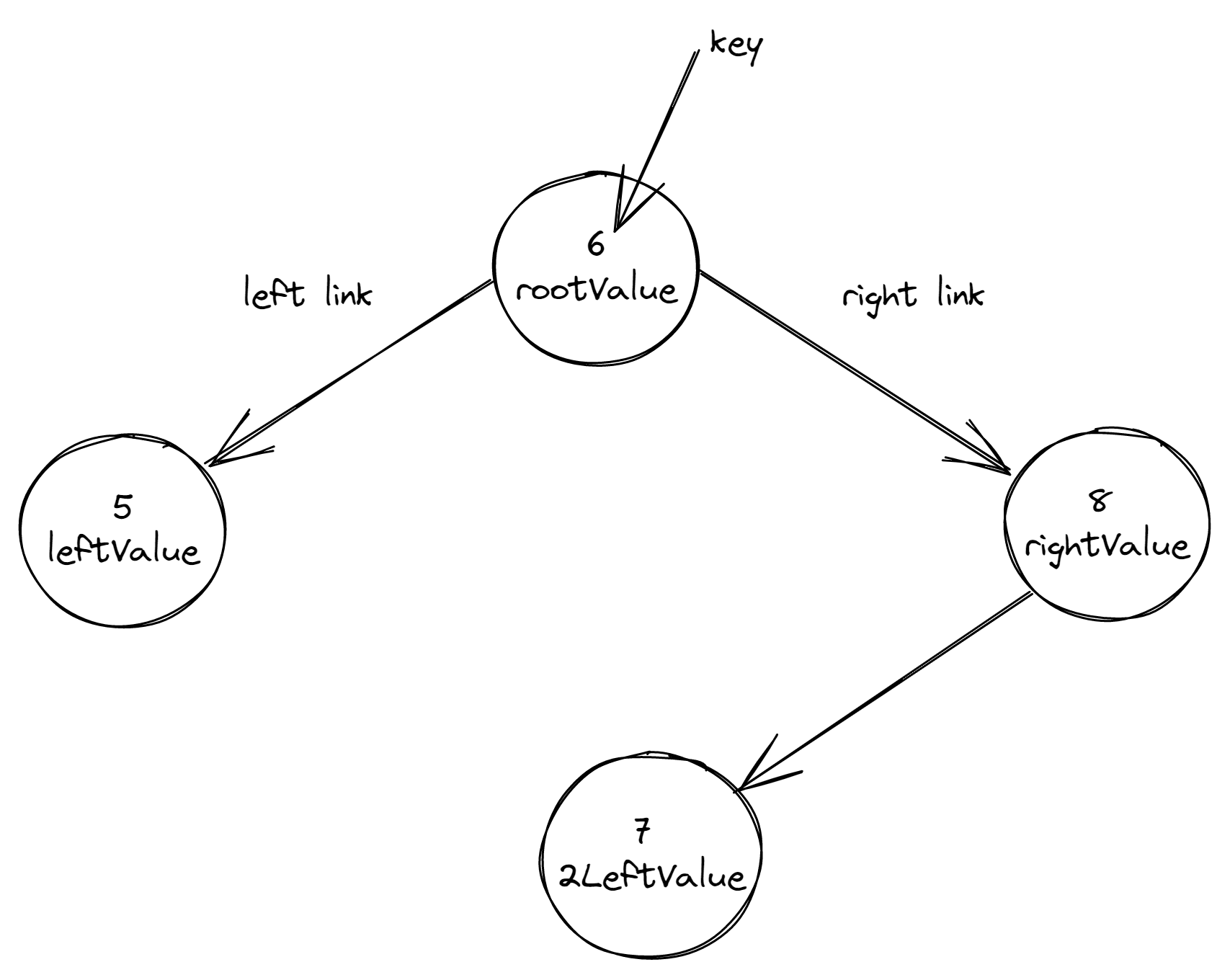
With test cases in place we can be confident in the implementation correctness:

    public int size() {
        return size(root);
    } 

    private int size(Node node) {
        if (node == null) {
            return 0;
        } else {
            return node.subtreeNodeNumber;
        }
    }

    public Value get(Key key) {
        return null;
    }

    public void put(Key key, Value value) {
        root = put(root, key, value);

    }

    private Node put(Node node, Key key, Value value) {
        if (node == null) {
            return new Node(key, value, 1);
        }
        int compare = key.compareTo(node.key);
        if (compare < 0) {
            node.left = put(node.left, key, value);
        } else if (compare > 0) {
            node.right = put(node.right, key, value);
        } else {
            node.value = value;
        }
        node.subtreeNodeNumber = size(node.left) + size(node.right) + 1;
        return node;
    }

GET

For get functionality we need to check if the correct value is returned for a given key and if key is not present null is returned:

    @Test
    void shouldGetRightValueForKey() {
        BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(RIGHT_KEY, RIGHT_VALUE);
        bst.put(SECOND_LEFT_KEY, SECOND_LEFT_VALUE);

        assertEquals(RIGHT_VALUE, bst.get(RIGHT_KEY));
    }

    @Test
    void shouldReturnNullWhenKeyIsNotPresent() {
            BinarySearchTree<Integer, String> bst = new BinarySearchTree<>();
        bst.put(ROOT_KEY, ROOT_VALUE);
        bst.put(RIGHT_KEY, RIGHT_VALUE);
        bst.put(SECOND_LEFT_KEY, SECOND_LEFT_VALUE);

        assertNull(bst.get(NON_PRESENT_KEY));
        }

In implementation recursive call for subtree will be used again:

    public Value get(Key key) {
        return get(root, key);
    }

    private Value get(Node node, Key key) {
        if (node == null) {
            return null;
        }
        int keyCmp = key.compareTo(node.key);
        if (keyCmp < 0) {
            return get(node.left, key);
        }
        if (keyCmp > 0) {
            return get(node.right, key);
        } else {
            return node.value;
        }
    }

Full implementation can be found on GitHub.

Sources: